Yuhi's Blog
丝之鸽
Yuhi
Great Hopes Make Everything Great Possible.
Github Email AcWing Codeforces
CC BY-NC 4.0

分块学习笔记

 ACM/Notes

学习笔记

分块思想

分块就是将一个序列分段来维护，比如有一个下标为 $[1,n]$ 的区间，我们将其分成几个大块每块大小为 $B$（当然未必是恰好，末尾可能会是一个小块），那么就有 $\lceil\frac{n}{B}\rceil$ 块。一般我们希望 $B$ 和 $\lceil\frac{n}{B}\rceil$ 差不多大，所以常取 $B=\sqrt{n}$ 。

我们能得到 / 需要维护的信息：

  • 下标 $i$ 的元素属于第 $(i-1)/B+1$ 块。
  • 块 $i$ 的左边界元素的下标为 $(i-1) \times B+1$，右边界元素下标为 $i\times B$ 。
  • 维护块 $i$ 的某种属性，比如可以用 $\text{delta}[i]$ 表示块 $i$ 中的所有元素的一个偏移量，比如用 $\text{sum}[i]$ 表示块 $i$ 中所有元素的和，等等...也可以用数据结构（树状数组，set，vector ）来维护每一个块的某些属性。

任取一段区间 $[l,r]$，一般会由中间的大块以及两边的小块构成。

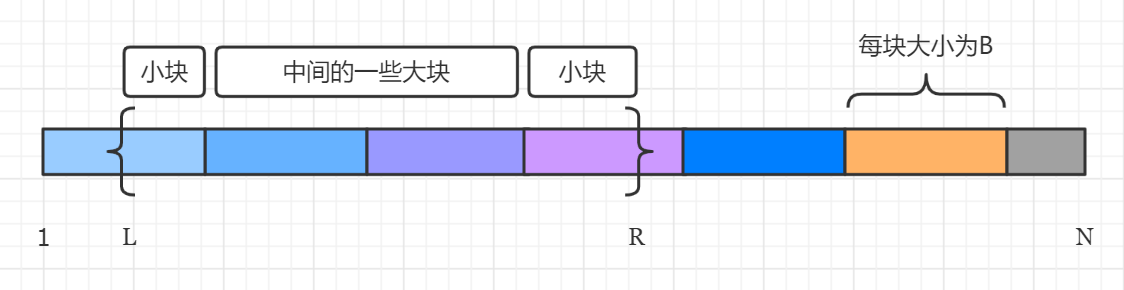
  • 左侧小块的下标区间为：$[l,\text{belong}[l]\times B]$
  • 右侧小块的下标区间为：$[(\text{belong}[r]-1)\times B+1,r]$
  • 中间大块的块编号区间为：$[\text{belong}[l]+1,\text{belong}[r]-1]$

分块处理区间问题的思路就是小块暴力，大块使用维护的属性，尤其注意需要特判 $[l,r]$ 属于同一块的情况。

预处理模板

  • $\mathrm{belong}[i]$ 表示下标 $i$ 所属于的块编号。
  • $B$ 表示每一块的大小，$sz$ 表示一共有多少块。
  • $\mathrm{L}[i],\mathrm{R}[i]$ 分别表示块 $i$ 的左闭边界和右闭边界。
1
2
3
4
5
6
7
8
9

int n, B, sz;
int belong[N], L[N], R[N];

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

例题

数列分块入门 9 题

原题链接

数列分块入门 1（区间加法，单点求值）

每块维护一个加法标记 $\mathrm{delta}[i]$ 即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 50010;

int n, B, sz;
int belong[N], L[N], R[N];
LL a[N], delta[N];

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

void add(int l, int r, int c) {
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) a[i] += c;
        return;
    }
    for (int i = l; i <= R[belong[l]]; i++) a[i] += c;
    for (int i = belong[l] + 1; i < belong[r]; i++) delta[i] += c;
    for (int i = L[belong[r]]; i <= r; i++) a[i] += c;
}

int main() {
    cin >> n;
    build();
    for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
    for (int i = 0; i < n; i++) {
        int op, l, r, c;
        scanf("%d%d%d%d", &op, &l, &r, &c);
        if (op == 0) add(l, r, c);
        else printf("%lld\n", a[r] + delta[belong[r]]);
    }
    return 0;
}

数列分块入门 2（区间加法，询问区间内小于某个值 $x$ 的元素个数）

每块维护加法标记，并用一个有序 vector 维护。区间加法操作，大块打标记，小块暴力修改以后需要重构其所在大块的有序 vector。查询操作大块二分，小块暴力。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 50010;

int n, B, sz;
int belong[N], L[N], R[N];
int a[N], delta[N];
vector<int> v[N];

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

void rebuild(int x) {
    v[x].clear();
    for (int i = L[x]; i <= R[x]; i++) v[x].push_back(a[i]);
    sort(v[x].begin(), v[x].end());
}

void add(int l, int r, int c) {
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) a[i] += c;
        rebuild(belong[l]);
        return;
    }
    for (int i = l; i <= R[belong[l]]; i++) a[i] += c;
    for (int i = belong[l] + 1; i < belong[r]; i++) delta[i] += c;
    for (int i = L[belong[r]]; i <= r; i++) a[i] += c;
    rebuild(belong[l]), rebuild(belong[r]);
}

int ask(int l, int r, int c) {
    int res = 0;
    LL x = 1ll * c * c;
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) {
            if (a[i] + delta[belong[l]] < x) res++;
        } 
        return res;
    }
    for (int i = l; i <= R[belong[l]]; i++) {
        if (a[i] + delta[belong[l]] < x) res++;
    }
    for (int i = belong[l] + 1; i < belong[r]; i++) {
        res += lower_bound(v[i].begin(), v[i].end(), x - delta[i]) - v[i].begin();
    }
    for (int i = L[belong[r]]; i <= r; i++) {
        if (a[i] + delta[belong[r]] < x) res++;
    }
    return res;
}

int main() {
    cin >> n;
    build();
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        v[belong[i]].push_back(a[i]);
    }
    for (int i = 1; i <= sz; i++) sort(v[i].begin(), v[i].end());
    for (int i = 0; i < n; i++) {
        int op, l, r, c;
        scanf("%d%d%d%d", &op, &l, &r, &c);
        if (!op) add(l, r, c);
        else printf("%d\n", ask(l, r, c));
    }
    return 0;
}

数列分块入门 3（区间加法，询问区间内小于某个值 x 的前驱（比其小的最大元素））

每块用一个有序 vector 维护，查询操作大块二分，小块暴力求小于 $x$ 的最大值，与大块二分得到的结果取 $\max$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 100010;

int n, B, sz;
int belong[N], L[N], R[N];
int a[N], delta[N];
vector<int> v[N];

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

void rebuild(int x) {
    v[x].clear();
    for (int i = L[x]; i <= R[x]; i++) v[x].push_back(a[i]);
    sort(v[x].begin(), v[x].end());
}

void add(int l, int r, int c) {
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) a[i] += c;
        rebuild(belong[l]);
        return;
    }
    for (int i = l; i <= R[belong[l]]; i++) a[i] += c;
    rebuild(belong[l]);
    for (int i = belong[l] + 1; i < belong[r]; i++) delta[i] += c;
    for (int i = L[belong[r]]; i <= r; i++) a[i] += c;
    rebuild(belong[r]);
}

int ask(int l, int r, int c) {
    int res = INT_MIN;
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) {
            if (a[i] + delta[belong[l]] < c)
                res = max(res, a[i] + delta[belong[l]]);
        }
        if (res == INT_MIN) res = -1;
        return res;
    }
    for (int i = l; i <= R[belong[l]]; i++) {
        if (a[i] + delta[belong[l]] < c)
            res = max(res, a[i] + delta[belong[l]]);
    }
    for (int i = belong[l] + 1; i < belong[r]; i++) {
        int pre = lower_bound(v[i].begin(), v[i].end(), c - delta[i]) - v[i].begin();
        if (--pre >= 0) res = max(res, v[i][pre] + delta[i]);
    }
    for (int i = L[belong[r]]; i <= r; i++) {
        if (a[i] + delta[belong[r]] < c)
            res = max(res, a[i] + delta[belong[r]]);
    }
    if (res == INT_MIN) res = -1;
    return res;
}

int main() {
    cin >> n;
    build();
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        v[belong[i]].push_back(a[i]);
    }
    for (int i = 1; i <= sz; i++) sort(v[i].begin(), v[i].end());
    for (int i = 0; i < n; i++) {
        int op, l, r, c;
        scanf("%d%d%d%d", &op, &l, &r, &c);
        if (!op) add(l, r, c);
        else printf("%d\n", ask(l, r, c));
    }
    return 0;
}

数列分块入门 4（区间加法，区间求和）

维护每块的和以及加法标记。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 50010;

int n, B, sz;
int belong[N], L[N], R[N];
int a[N], delta[N];
LL sum[N];

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

void add(int l, int r, int c) {
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) a[i] += c, sum[belong[l]] += c;
        return;
    }
    for (int i = l; i <= R[belong[l]]; i++) a[i] += c, sum[belong[l]] += c;
    for (int i = belong[l] + 1; i < belong[r]; i++) delta[i] += c, sum[i] += 1ll * B * c;
    for (int i = L[belong[r]]; i <= r; i++) a[i] += c, sum[belong[r]] += c;
}

int query(int l, int r, int c) {
    LL mod = c + 1;
    LL res = 0;
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) (res += a[i] + delta[belong[l]]) %= mod;
        return res;
    }
    for (int i = l; i <= R[belong[l]]; i++) (res += a[i] + delta[belong[l]]) %= mod;
    for (int i = belong[l] + 1; i < belong[r]; i++) (res += sum[i]) %= mod;
    for (int i = L[belong[r]]; i <= r; i++) (res += a[i] + delta[belong[r]]) %= mod;
    return res;
}

int main() {
    cin >> n;
    build();
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        sum[belong[i]] += a[i];
    }
    for (int i = 0; i < n; i++) {
        int op, l, r, c;
        scanf("%d%d%d%d", &op, &l, &r, &c);
        if (!op) add(l, r, c);
        else printf("%d\n", query(l, r, c));
    }
    return 0;
}

数列分块入门 5（区间开方，区间求和）

由于数据范围可知，每个数开方几次就会变成 $1$ 或者是 $0$（初始就是 $0$ ）。那么只需要对每一个大块打一个标记，表示该大块是否只含有 $01$，这样的大块就不需要开方了。同时维护每一个大块的和 $\mathrm{sum}[i]$。查询区间和的操作不变。区间开方时，小块暴力开方，大块首先判断是否需要开方，如果不需要就跳过，如果需要就暴力开方，同时更新 $\mathrm{sum}[i]$ 的值，如果全部化成了 $01$ 就更新标记。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 50010;

int n, B, sz;
int belong[N], L[N], R[N];
int a[N];
LL sum[N];
bool st[N]; // st[i]=true表示第i块中只含有01不需要再开方

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

LL ask(int l, int r) {
    LL res = 0;
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) res += a[i];
        return res;
    }
    for (int i = l; i <= R[belong[l]]; i++) res += a[i];
    for (int i = belong[l] + 1; i < belong[r]; i++) res += sum[i];
    for (int i = L[belong[r]]; i <= r; i++) res += a[i];
    return res;
}

void gao(int l, int r) {
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) {
            sum[belong[l]] -= a[i]; 
            a[i] = sqrt(a[i]);
            sum[belong[l]] += a[i];
        }
        return;
    }
    for (int i = l; i <= R[belong[l]]; i++) {
        sum[belong[l]] -= a[i]; 
        a[i] = sqrt(a[i]);
        sum[belong[l]] += a[i];
    }
    for (int i = belong[l] + 1; i < belong[r]; i++) {
        if (st[i]) continue; // 已经只含有01，不需要开方了
        bool flag = true; // 假设第i块已经全部只含有0和1
        sum[i] = 0; // 重新计算和
        for (int j = L[i]; j <= R[i]; j++) {
            a[j] = sqrt(a[j]);
            sum[i] += a[j];
            if (a[j] > 1) flag = false;
        }
        st[i] = flag;
    }
    for (int i = L[belong[r]]; i <= r; i++) {
        sum[belong[r]] -= a[i]; 
        a[i] = sqrt(a[i]);
        sum[belong[r]] += a[i];
    }
}

int main() {
    cin >> n;
    build();
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        sum[belong[i]] += a[i];
    }
    for (int i = 0; i < n; i++) {
        int op, l, r, c;
        scanf("%d%d%d%d", &op, &l, &r, &c);
        if (!op) gao(l, r);
        else printf("%lld\n", ask(l, r));
    }
    return 0;
}

数列分块入门 6（单点插入，单点询问）

每块用 vector 维护，每次插入或查询根据遍历每个 vector 块大小来定位插入位置所在块。如果插入后，该块大小到达一个上限，比如 $5$ 倍的最初设置块大小，就重新分块。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 300010;

int n, B, sz;
int belong[N];
int a[N];
vector<int> v[N];

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
}

void rebuild() {
    n = 0;
    for (int i = 1; i <= sz; i++) {
        for (auto x : v[i]) a[++n] = x;
        v[i].clear();
    }
    build();
    for (int i = 1; i <= n; i++) v[belong[i]].push_back(a[i]);
}

void insert(int l, int x) {
    int idx = 1;
    while (l > v[idx].size()) l -= v[idx++].size();
    // 此时l属于块idx
    // 在第idx块中下标l-1位置插入x
    v[idx].insert(v[idx].begin() + l - 1, x);
    if (v[idx].size() > 5 * B) rebuild();
}

int query(int r) {
    int idx = 1;
    while (r > v[idx].size()) r -= v[idx++].size();
    return v[idx][r - 1];
}

int main() {
    cin >> n;
    build();
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        v[belong[i]].push_back(a[i]);
    }
    int m = n;
    while (m--) {
        int op, l, r, c;
        scanf("%d%d%d%d", &op, &l, &r, &c);
        if (!op) insert(l, r);
        else printf("%d\n", query(r));
    }
    return 0;
}

数列分块入门 7（区间乘法，区间加法，单点询问）

和线段树同时维护区间和以及区间乘法做法类似，对每个大块维护两个懒标记 lazy_mul[i] 和 lazy_add[i]，表示块 i 的所有数的实际值，都在原来的基础上先乘以 lazy_mul[i] 再加上 lazy_add[i]。题目中的两个操作可以统一为：某个区间内的所有数需要先乘以一个数再加上一个数字（加法操作转化为先乘以 1 再加法，乘法操作转化为先乘法再加上 0 ）。对于大块 i 而言，现在要让其中所有数先乘以 mul 再加上 add，只需要修改懒标记，更新方式如下：

1
2

lazy_mul[i] = lazy_mul[i] * mul;
lazy_add[i] = lazy_add[i] * mul + add;

对于小块，那么进行暴力修改原数组即可。在此之前，必须先将小块所属于的大块 rebuild，即将 $2$ 种标记的效果执行到原数组上，此后再进行暴力修改该数组，进行乘法和加法操作。最后，注意各种中间过程取模。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 100010, mod = 10007;

int n, B, sz;
int belong[N], L[N], R[N];
LL a[N];
LL lazy_add[N], lazy_mul[N];

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

// 清空第x块的标记
void rebuild(int x) {
    for (int i = L[x]; i <= R[x]; i++) {
        a[i] = (1ll * a[i] * lazy_mul[x] + lazy_add[x]) % mod; 
    }
    lazy_add[x] = 0, lazy_mul[x] = 1;
}

// [l, r]区间乘以mul加上add
void gao(int l, int r, int mul, int add) {
    if (belong[l] == belong[r]) {
        rebuild(belong[l]); // 先将标记清空
        // 暴力修改[l,r]乘以mul加上add
        for (int i = l; i <= r; i++) {
            a[i] = (1ll * a[i] * mul + add) % mod; 
        }
        return;
    }
    rebuild(belong[l]);
    for (int i = l; i <= R[belong[l]]; i++) {
        a[i] = (1ll * a[i] * mul + add) % mod; 
    }
    for (int i = belong[l] + 1; i < belong[r]; i++) {
        lazy_mul[i] = lazy_mul[i] * mul % mod;
        lazy_add[i] = (lazy_add[i] * mul + add) % mod;
    }
    rebuild(belong[r]);
    for (int i = L[belong[r]]; i <= r; i++) {
        a[i] = (1ll * a[i] * mul + add) % mod; 
    }
}

// 返回a[r]的值
int ask(int x) {
    return (1ll * a[x] * lazy_mul[belong[x]] + lazy_add[belong[x]]) % mod;
}

int main() {
    cin >> n;
    build();
    for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
    for (int i = 1; i <= sz; i++) {
        lazy_add[i] = 0, lazy_mul[i] = 1;
    }
    for (int i = 0; i < n; i++) {
        int op, l, r, c;
        scanf("%d%d%d%d", &op, &l, &r, &c);
        if (!op) gao(l, r, 1, c); // 乘以1再加上c
        else if (op == 1) gao(l, r, c, 0); // 乘以c再加上0
        else printf("%d\n", ask(r));
    }
    return 0;
}

数列分块入门 8（区间询问等于一个数 c 的元素，并将这个区间的所有元素改为 c）

对每块维护一个 st[i]，true 则表示大块中的所有元素值相同，此时 val[i] = x 表示第 i 块所有元素均为 x。小块暴力枚举，并重构其所属大块，对于大块直接看标记计算答案，如果 st[i] 为 false 则暴力枚举块内元素，计算答案，最后更新该大块的 st[i] 为 true 即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 100010;

int n, B, sz;
int belong[N], L[N], R[N];
int a[N], val[N];
bool st[N];

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

// 不完整的小块[l,r]区间求解
void solve(int l, int r, int c, int &res) {
    if (l > r) return;
    if (st[belong[l]]) { // 如果l所在大块均为一个值
        if (val[belong[l]] == c) {
            res += r - l + 1;
        } else {
            // 重构该块
            for (int i = L[belong[l]]; i < l; i++) a[i] = val[belong[l]];
            for (int i = l; i <= r; i++) a[i] = c;
            for (int i = r + 1; i <= R[belong[r]]; i++) a[i] = val[belong[l]];
            st[belong[l]] = 0;
        }
    } else {
        for (int i = l; i <= r; i++) {
            if (a[i] == c) res++;
            else a[i] = c;
        }
        bool flag = true;
        for (int i = L[belong[l]]; i < l; i++) {
            if (a[i] != c) {
                flag = false;
                break;
            }
        }
        if (!flag) return;
        for (int i = r + 1; i <= R[belong[r]]; i++) {
            if (a[i] != c) {
                flag = false;
                break;
            }
        }
        if (!flag) return;
        st[belong[l]] = 1, val[belong[l]] = c;
    }
}

int query(int l, int r, int c) {
    int res = 0;
    if (belong[l] == belong[r]) {
        solve(l, r, c, res);
        return res;
    }
    solve(l, R[belong[l]], c, res);
    for (int i = belong[l] + 1; i < belong[r]; i++) {
        if (st[i]) {
            if (val[i] == c) res += B;
            else val[i] = c;
        } else {
            for (int j = L[i]; j <= R[i]; j++) res += a[j] == c;
            st[i] = 1, val[i] = c;
        }
    }
    solve(L[belong[r]], r, c, res);
    return res;
}

int main() {
    cin >> n;
    build();
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
    for (int i = 0; i < n; i++) {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        printf("%d\n", query(l, r, c));
    }
    return 0;
}

数列分块入门 9（区间的最小众数）

区间 $[l, r]$ 的众数，一定是在两边的小块中出现的数，或者是中间连续的大块区域的众数，那么待选答案就有 $O(\sqrt{n})$ 个，对于每一个待选答案 $x$，我们需要求它在 $[l, r]$ 区间出现的次数，来确定最终答案。

有两种做法，$\texttt{Solution 1}$ 是预处理一个前缀和 $s[i][j]$ 表示前 $1\text{~}i$ 块中 $j$ 出现的次数，小块暴力统计，大块差分。$\texttt{Solution 2}$ 是用 vector 存每一个数 $x$ 出现的所有下标。然后在对应的 vector 中二分查包含在 $[l, r]$ 区间中的下标个数。

对于中间连续的大块区域的众数，可以预处理 $f[i][j]$ 表示第 $i\text{~}j$ 块的众数。枚举每一块 $i$，然后枚举 $j$ 从该块的左边界 $\text{L}[i]$ 一直枚举到 $n$，用哈希表统计一下出现每个数出现次数，同时维护答案 $res$，然后每当 $j$ 到达某一块的右边界即 $j == \text{R}[\mathrm{belong}[j]]$ 时候记录答案 $res$ 到 $f[i][\text{belong}[j]]$ 中，表示 $i\text{~}\text{belong}[j]]$ 块的众数为 $res$ 。预处理 $f[i][j]$ 的复杂度为 $O(n\sqrt{n})$ 。

块大小取 $B = \frac{n}{\sqrt{m \times \log_2{n}}}$ 。

$\texttt{Solution 1}$
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94

#include <bits/stdc++.h>

using namespace std;

const int N = 40010, M = 3010;

int n, m, B, sz;
int belong[N], L[N], R[N];
int f[M][M]; // f[i][j]表示i~j块的众数
int s[M][N]; // s[i][j]表示前1~i块中j出现的次数
int a[N], cnt[N];
vector<int> alls; // 离散化
int lim; // 离散化后的编号为0~lim

void build() {
    B = n / sqrt(m * log2(n)), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

// 返回x离散化后的编号
int find(int x) {
    return lower_bound(alls.begin(), alls.end(), x) - alls.begin();
}

// 求大块l~r中x出现的次数
int get(int l, int r, int x) {
    return s[r][x] - s[l - 1][x];
}

// 用可能的答案x来更新[l, r]的最小众数
void update(int x, int l, int r, int &res, int &res_cnt) {
    int lcnt = 0, rcnt = 0; // 分别表示x在左右小块中出现的次数
    for (int i = l; i <= R[belong[l]]; i++) lcnt += a[i] == x;
    for (int i = L[belong[r]]; i <= r; i++) rcnt += a[i] == x;
    int mcnt = get(belong[l] + 1, belong[r] - 1, x);
    int xcnt = lcnt + rcnt + mcnt; // xcnt表示x在[l,r]区间出现的次数
    if (xcnt > res_cnt || xcnt == res_cnt && x < res) res = x, res_cnt = xcnt;
}

// [l,r]区间最小众数
int query(int l, int r) {
    int res = INT_MAX, res_cnt = 0;
    if (belong[l] == belong[r]) { 
        for (int i = l; i <= r; i++) { // 暴力求最小众数
            cnt[a[i]]++;
            if (cnt[a[i]] > res_cnt || cnt[a[i]] == res_cnt && a[i] < res) res = a[i], res_cnt = cnt[a[i]];
        }
        for (int i = l; i <= r; i++) cnt[a[i]]--;
        return alls[res]; // 返回实际值
    }
    for (int i = l; i <= R[belong[l]]; i++) update(a[i], l, r, res, res_cnt);
    if (belong[l] + 1 <= belong[r] - 1) update(f[belong[l] + 1][belong[r] - 1], l, r, res, res_cnt);
    for (int i = L[belong[r]]; i <= r; i++) update(a[i], l, r, res, res_cnt);
    return alls[res];
}

int main() {
    cin >> n >> m;
    build();
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        alls.push_back(a[i]);
    }
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    lim = alls.size() - 1;
    // 将a[i]更新为离散化后的值
    for (int i = 1; i <= n; i++) a[i] = find(a[i]);
    // 预处理s[][]
    for (int i = 1; i <= sz; i++) {
        for (int j = 0; j <= lim; j++) s[i][j] = s[i - 1][j];
        for (int j = L[i]; j <= R[i]; j++) s[i][a[j]]++;
    }
    // 预处理f[][]
    for (int i = 1; i <= sz; i++) {
        int res = INT_MAX, res_cnt = 0; // res表示众数，res_cnt为出现次数
        for (int j = L[i]; j <= n; j++) {
            cnt[a[j]]++;
            if (cnt[a[j]] > res_cnt || cnt[a[j]] == res_cnt && a[j] < res) res = a[j], res_cnt = cnt[a[j]];
            if (j == R[belong[j]]) f[i][belong[j]] = res;
        }
        for (int j = L[i]; j <= n; j++) cnt[a[j]]--;
    }
    int last = 0;
    while (m--) {
        int l, r; scanf("%d%d", &l, &r);
        l = (l + last - 1) % n + 1, r = (r + last - 1) % n + 1;
        if (l > r) swap(l, r);
        printf("%d\n", last = query(l, r));
    }
    return 0;
}
$\texttt{Solution 2}$
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95

#include <bits/stdc++.h>

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 100010, M = 2010;

int n, m, B, sz;
int belong[N], L[N], R[N];
int a[N];
int mode[M][M]; // mode[i][j]表示大块i~j区域的众数
vector<int> v[N];
vector<int> alls;
int mp[N];          

void build() {
    B = n / sqrt(n * log2(n)), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

// 离散化后x的编号
int find(int x) {
    return lower_bound(alls.begin(), alls.end(), x) - alls.begin();
}

// 暴力求[l,r]区间的众数，返回其离散化值
int force_mode(int l, int r) {
    memset(mp, 0, sizeof mp);
    int res = N - 1, cnt = 0;
    for (int i = l; i <= r; i++) {
        mp[a[i]]++;
        if (mp[a[i]] > cnt || mp[a[i]] == cnt && a[i] < res) res = a[i], cnt = mp[a[i]];
    }
    return res; // 返回实际众数值的离散化后的值
}

// 查找离散化值为x的元素在下标区间[l,r]出现次数
int calc(int x, int l, int r) {
    return upper_bound(v[x].begin(), v[x].end(), r) - lower_bound(v[x].begin(), v[x].end(), l);
}

// 用待选众数x来更新[l, r]区间的实际众数res，其出现次数为cnt
void solve(int x, int l, int r, int &res, int &cnt) {
    int xcnt = calc(x, l, r); // x在[l,r]区间出现的次数
    if (xcnt > cnt || xcnt == cnt && x < res) res = x, cnt = xcnt;
}

// 返回[l,r]区间众数
int query(int l, int r) {
    int res = N - 1, cnt = 0; // res为实际众数的离散化值,cnt为众数出现次数
    if (belong[l] == belong[r]) {
        solve(force_mode(l, r), l, r, res, cnt);
        return alls[res];
    }
    for (int i = l; i <= R[belong[l]]; i++) solve(a[i], l, r, res, cnt);
    if (belong[l] + 1 < belong[r]) solve(mode[belong[l] + 1][belong[r] - 1], l, r, res, cnt);
    for (int i = L[belong[r]]; i <= r; i++) solve(a[i], l, r, res, cnt);
    return alls[res];
}

int main() {
    scanf("%d", &n);
    build();
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        alls.push_back(a[i]);
    }
    // 离散化
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    for (int i = 1; i <= n; i++) {
        a[i] = find(a[i]);
        v[a[i]].push_back(i); // 存每一个a[i]出现的所有下标位置
    }
    // 初始化任意两个大块之间区域的众数
    for (int i = 1; i <= sz; i++) {
        int res = N - 1, cnt = 0;
        memset(mp, 0, sizeof mp);
        for (int j = L[i]; j <= n; j++) {
            mp[a[j]]++;
            if (mp[a[j]] > cnt || mp[a[j]] == cnt && a[j] < res) res = a[j], cnt = mp[a[j]]; 
            mode[i][belong[j]] = res;
        }
    }
    for (int i = 0; i < n; i++) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", query(l, r));
    }
    return 0;
}

Codeforces785E Anton and Permutation

原题链接

题意：动态逆序对问题。给定一个初始状态为 $\text{1~n}$ 的排列，每次操作交换其中的两个数，并输出操作后当前序列的逆序对个数。

解法：qwq 咕咕咕。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

#include <bits/stdc++.h>

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 200010, M = 510;

int n, k, B;
int a[N];
int belong[N]; // belong[i]表示下标i属于第几块
vector<int> v[M]; // v[i]维护第i块的有序序列
LL res;

LL solve(int l, int r) {
    if (l == r) return 0;
    int x = a[l], y = a[r];
    if (x > y) swap(x, y);
    LL cnt = 0;
    // 处理交换，在l,r各自大块中修改，以及原序列a中交换
    // 先记录需要修改的位置k1,k2，否则如果l,r在同一块可能产生问题
    int k1 = find(v[belong[l]].begin(), v[belong[l]].end(), a[l]) - v[belong[l]].begin();
    int k2 = find(v[belong[r]].begin(), v[belong[r]].end(), a[r]) - v[belong[r]].begin();
    v[belong[l]][k1] = a[r], v[belong[r]][k2] = a[l];
    sort(v[belong[l]].begin(), v[belong[l]].end());
    sort(v[belong[r]].begin(), v[belong[r]].end());
    swap(a[l], a[r]);
    // 计算逆序对数量的变化，注意上面已经交换了a[l]和a[r]
    // 在[l+1,r-1]下标区间查找在值域区间[x+1,y-1]之间个数cnt
    // 答案加上cnt*2+1,如果x>y就减去cnt*2+1
    if (belong[l + 1] == belong[r - 1]) {
        for (int i = l + 1; i < r; i++)
            if (a[i] > x && a[i] < y) cnt++;
    } else {
        // 处理左侧小块
        for (int i = l + 1; i < (belong[l + 1] + 1) * B; i++) {
            if (a[i] > x && a[i] < y) cnt++;
        }
        // 处理大块
        for (int i = belong[l + 1] + 1; i < belong[r - 1]; i++) {
            cnt += upper_bound(v[i].begin(), v[i].end(), y - 1) 
                 - lower_bound(v[i].begin(), v[i].end(), x + 1);
        }
        // 处理右侧小块
        for (int i = belong[r - 1] * B; i < r; i++) {
            if (a[i] > x && a[i] < y) cnt++;
        }
    }
    return (cnt * 2 + 1) * (a[l] > a[r] ? 1 : -1);
}

int main() {
    cin >> n >> k;
    B = sqrt(N); // emm为啥取n就wa50了呢
    for (int i = 1; i <= n; i++) {
        a[i] = i;
        belong[i] = i / B;
        v[belong[i]].push_back(i);
    }
    while (k--) {
        int l, r; scanf("%d%d", &l, &r);
        if (l > r) swap(l, r);
        res += solve(l, r);
        cout << res << endl;
    }
    return 0;
}

AcWing263 作诗

原题链接

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <bits/stdc++.h>

using namespace std;

const int N = 100010, M = sqrt(N) + 10;

int n, c, m, B, sz;
int belong[N], L[M], R[M];
int a[N], s[M][N]; // s[i][j]表示前1~i块中j出现的次数
int f[M][M]; // f[i][j] 表示i~j块中出现次数为正偶数的不同的数的个数
int cnt[N]; // cnt[i]表示i出现的次数

void build() {
    B = sqrt(n), sz = (n - 1) / B + 1;
    for (int i = 1; i <= n; i++) belong[i] = (i - 1) / B + 1;
    for (int i = 1; i <= sz; i++) L[i] = (i - 1) * B + 1, R[i] = L[i] + B - 1;
    R[sz] = n;
}

// x在[l,r]块中出现的次数
int get(int l, int r, int x) {
    return s[r][x] - s[l - 1][x];
}

// [l,r]之间出现次数为正偶数次的不同的数的个数
int query(int l, int r) {
    int res = 0;
    if (belong[l] == belong[r]) {
        for (int i = l; i <= r; i++) {
            cnt[a[i]]++;
            if (cnt[a[i]] % 2 == 0) res++;
            else if (cnt[a[i]] > 1) res--;
        }
        for (int i = l; i <= r; i++) cnt[a[i]]--;
        return res;
    }
    res = f[belong[l] + 1][belong[r] - 1];
    for (int i = l; i <= R[belong[l]]; i++) {
        cnt[a[i]]++;
        int t = get(belong[l] + 1, belong[r] - 1, a[i]);
        int x = cnt[a[i]] + t;
        if (x % 2 == 0) res++;
        else if (x > 1) res--;
    }
    for (int i = L[belong[r]]; i <= r; i++) {
        cnt[a[i]]++;
        int t = get(belong[l] + 1, belong[r] - 1, a[i]);
        int x = cnt[a[i]] + t;
        if (x % 2 == 0) res++;
        else if (x > 1) res--;
    }
    for (int i = l; i <= R[belong[l]]; i++) cnt[a[i]]--;
    for (int i = L[belong[r]]; i <= r; i++) cnt[a[i]]--;
    return res;
}

int main() {
    cin >> n >> c >> m;
    build();
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
    for (int i = 1; i <= sz; i++) {
        for (int j = 1; j <= c; j++) s[i][j] = s[i - 1][j];
        for (int j = L[i]; j <= R[i]; j++) s[i][a[j]]++;
    }
    for (int i = 1; i <= sz; i++) {
        int ans = 0; // ans表示起始块为i时，到每一个结束块之间的答案
        for (int j = L[i]; j <= n; j++) {
            cnt[a[j]]++;
            if (cnt[a[j]] % 2 == 0) ans++;
            else if (cnt[a[j]] > 1) ans--;
            if (j == R[belong[j]]) f[i][belong[j]] = ans;
        }
        for (int j = L[i]; j <= n; j++) cnt[a[j]]--;
    }
    int last = 0;
    while (m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        l = (l + last) % n + 1;
        r = (r + last) % n + 1;
        if (l > r) swap(l, r);
        printf("%d\n", last = query(l, r));
    }
    return 0;
}

学习资料

  1. 肖然大佬的例题讲解
  2. 卿学姐的分块模板讲解
updatedupdated2020-11-232020-11-23
a9d3b65
first commit
Edit Me?

相关文章：

加载评论
点击刷新