Manacher 算法详解

本文介绍字符串——回文串——Manacher 算法。

写在前面

众所周知，最长回文子串问题可由二分+哈希或者后缀数组等求解。本文将不再介绍暴力算法以及上述两种算法。
Manacher 算法是处理回文串的利器，由一位名叫 Manacher 的大佬在 1975 年提出，可在线性时间复杂度内求解出最长回文子串。

问题

给定一个字符串 $S$ ，求出它的最长回文子串长度。
比如 $ababbac$ 的最长回文子串为 $abba$ ，长度为 $4$ 。

Manacher 算法

字符串预处理

为了解决奇数长度的回文串，与偶数长度的回文串的不统一的问题，我们对给定字符串S预处理，即间隔插入分隔符#，如下所示：

1
2
3
4
5
原串 abaa -> #a#b#a#a#
最长回文子串 aba -> #a#b#a#

原串 abaabc -> #a#b#a#a#b#c
最长回文子串 baab -> #b#a#a#b#

那么所有回文子串都统一成了奇数长度。

引入 p 数组, rt, mid

预处理后的新串表示为Str，定义数组p[]，p[i]表示 Str中以下标i为回文中心的最大回文半径。以abab为例：

i	1	2	3	4	5	6	7	8	9
Str	#	a	#	b	#	a	#	b	#
p[i]	1	2	1	4	1	4	1	2	1

如果我们得到了 p[i]，那么 p[i] - 1 就是原串 $\rm S$ 以 i 为回文中心的最大回文长度（可根据上表验证一下）。

现在我们来求解 p[i]，定义 rt 表示已经计算过的回文串能达到的最远右边界的下一个位置^[1]。即 $\textrm{rt} = \max(j+p[j]),j\in[1,i-1]$，mid 表示 rt 所对应的最左侧的回文中心，有 mid + p[mid] == rt 。如下图所示：

◎ mid 与 rt 的定义

计算 p 数组, 更新 rt, mid

如何计算 p[i] 呢，显然有 i > mid（因为 p[mid] 已经计算过）下面再分两种情况讨论：
情况一：i < rt

◎ i < rt 时计算 p[i]

此时我们发现，我们可以用已知的 p[j] 的信息来辅助计算 p[i]。p[j] 又有两种情况，讨论如下：

以 j 为中心的最大回文串被包含在以 mid 为中心的最大回文串中

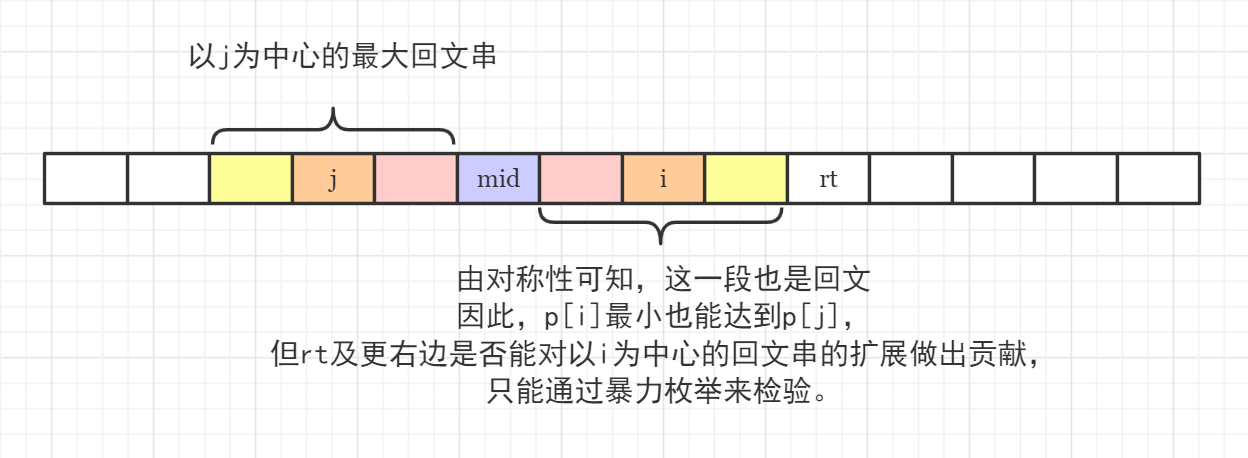◎ 以 j 为中心的最大回文串被包含在以 mid 为中心的最大回文串中

以 j 为中心的最大回文串没有被包含在以 mid 为中心的最大回文串中

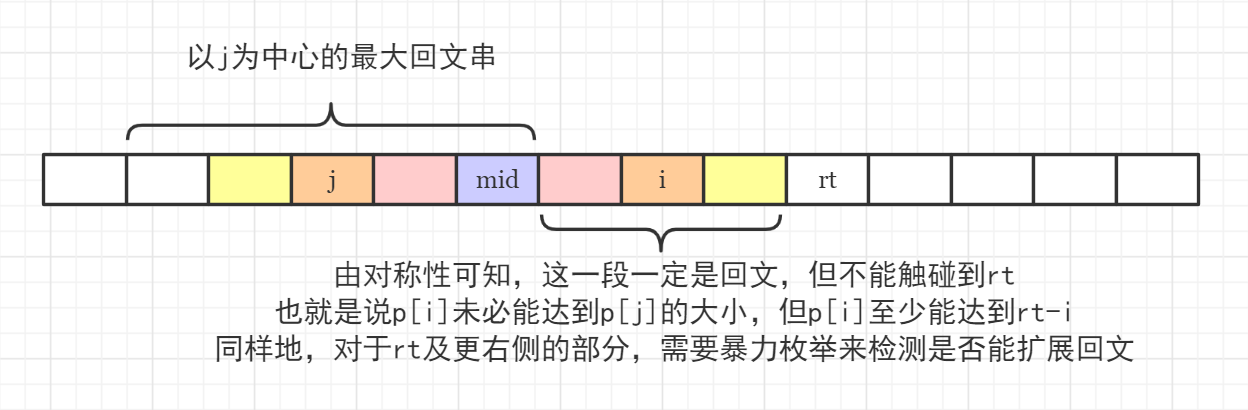◎ 以 j 为中心的最大回文串没有被包含在以 mid 为中心的最大回文串中

根据以上两种情况，可以写出如下代码：

1
2
if (i < rt) p[i] =  min(p[2 * mid - i], rt - i); /* j = 2 * mid - i */ 
while (str[i + p[i]] == str[i - p[i]]) p[i]++; /* 暴力扩展（后面会用到哨兵，因此不需要考虑边界） */

情况二：i >= rt 此时，没有已知信息可以辅助计算了，令 p[i] = 1 然后暴力扩展。

◎ i >= rt 时计算 p[i]

根据上述分析，可以写出如下代码：

1
2
if (i >= rt) p[i] = 1;
while (str[i + p[i]] == str[i - p[i]]) p[i]++; /* 暴力扩展（后面会用到哨兵，因此不需要考虑边界） */

求解出 p[i] 以后，需要更新 mid 和 rt，代码如下：

1
2
3
4
if (i + p[i] > rt) { /* 如果以i为中心的最大回文串能更新rt */
    rt = i + p[i];
    mid = i; /* 更新rt对应的mid */
}

完整代码

题目链接：AcWing 139. 回文子串的最大长度

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 2000010;

int n, m, Case;
char s[N], str[N];
int p[N];

void manacher() {
    int rt = 0, mid = 0;
    int res = 0;
    for (int i = 1; i <= m; i++) {
        p[i] = i < rt ? min(p[2 * mid - i], rt - i) : 1;
        while (str[i + p[i]] == str[i - p[i]]) p[i]++;
        if (i + p[i] > rt) {
            rt = i + p[i];
            mid = i;
        }
        res = max(res, p[i] - 1);
    }
    printf("Case %d: %d\n", ++Case, res);
}

int main() {
    str[0] = '!', str[1] = '#'; /* str[0]为哨兵 */
    while (scanf("%s", s), s[0] != 'E') {
        n = strlen(s);
        for (int i = 0; i < n; i++) {
            str[i * 2 + 2] = s[i];
            str[i * 2 + 3] = '#';
        }
        m = n * 2 + 1;
        str[m + 1] = '@';  /* 哨兵 */   
        manacher();
    }
    return 0;
}

细节解释
细心的你可能发现了，在预处理字符串时，其实是将原串，比如 abab，处理成了 !#a#b#a#b#@。下标 0 位置和末尾取了没有出现过的字符且首尾不相等，作为哨兵，就不用考虑边界啦。

时间复杂度分析

很显然暴力扩展只发生在 rt 及右侧，且每次暴力扩展成功后都会将 rt 更新到暴力扩展最终失败的位置，rt 就增大。所以暴力扩展的总次数是线性的，因此 Manacher 算法的总时间复杂度为 $\mathcal{O}(n)$，其实以上都是口胡（逃。

参考资料

这里很多博客都写的不严谨，并不是说取右闭边界不可以，而是很多文章在这里对 rt 的定义与后面给出的代码不对应，容易给读者带来困惑。

Manacher 算法详解

写在前面

Manacher 算法

字符串预处理

引入 p 数组, rt, mid

计算 p 数组, 更新 rt, mid

完整代码

时间复杂度分析

参考资料

相关文章：